Octave clustering demo part 5: hierarchical clustering
[This post is part of the Octave clustering demo series]
So, if you read this you probably have already unpacked the tgz file containing the demo and read the previous article about k-medoids clustering. If you want to check out the older Octave clustering articles, here they are: part 0 - part 1 - part 2 - part 3.
Run the hierarchicalDemo script (if launched without input parameters, it will open the "crescents.mat" data file by default). The script will plot the dataset, then it will try to perform clustering using first k-means and then an agglomerative hierarchical clustering algorithm. Run the algorithm with all the datasets available (note that you will need to modify the code to make it work with different numbers of clusters).
Questions:
- how does k-means perform on the non-globular datasets (crescents, circles01, and circles02)? What is the reason of this performance? how does hierarchical algorithm perform instead?
- now let us play with the "agglomerative" dataset. Information is missing so you know neither the number of clusters in advance nor the ground truth about points (i.e. which class they belong to). First of all, run the hclust function with different numbers of clusters and plot the results. Are you satisfied with them? What do you think is the reason of this "chaining" phenomenon?
- complete the code in hclust.m so it also calculates complete and average linkage, and run the algorithm again. How do clustering results change? Plot and comment them.
Octave clustering demo part 4: k-Medoids
[This post is part of the Octave clustering demo series]
Here follows the description of the first of two new Octave clustering demos. If you have attended the PAMI class this year you probably know what I am talking about. If instead you are new to these demos please (1) check the page linked above and (2) set up your Octave environment (feel free to download the old package and play with the old demos too ;-)). Then download this new package.
Run the kMedoidsDemo script (if launched without input parameters, it will open the "noisyBlobs01.mat" data file by default). The script will plot the dataset, then it will try to perform clustering using first k-means and then k-medoids. Run the experiment many times (at least 4-5 times) for each of the three noisyBlobs datasets (you can pass the dataset path and name as a parameter to the kMedoidsDemo function).
Questions:
- comment the "worst case" results you get from k-means: what happens and how does noise influence this behavior?
- compare the results you get with k-means with the ones you get with k-medoids: how does k-medoids deal with the presence of noise?
- what would happen if noise points were much farther from the original clusters? Try to get few (1-2) of them and bring them very far from the rest of the data… what are the results you get from k-means and k-medoids?
Hints:
- the demo stops at each step waiting for you to press a key. You can disable this feature by setting the "interactive" variable to zero at the beginning of the script;
- there are two different k-means implementations you can run: feel free to try both just by uncommenting their respective code.
WordPress in a (Virtual)box
Looking for some cool material for a new class at SUPSI DFA, I recently had a chance to experiment with Virtual Appliances. The main idea is the following: to setup most Web applications you need not only the applications themselves, but a whole set of softwares they depend on, (e.g. a web server, a database, a language interpreter), some additional apps to manage your data (e.g. phpMyAdmin to administer your MySQL database), and of course configurations for all of them; a virtual appliance is a self-contained virtual machine where everything, from the OS to every bit of code you need, is already installed and configured so that you won't need to worry about setting up your system, but you will be immediately able to start working with it.
There exist different VA providers, such as Bitnami, Turnkey Linux, and JumpBox. Each one has its own peculiarities: for instance, JumpBox uses proprietary software (as far as I learned from here) and to get VA images you need to pay a subscription; Bitnami does not only provide virtual machines, but also native installers for Windows, Linux, and Mac, and all of these are free; TKL, also free, is oriented to more technical users and should be better if you plan to extend the VA with other services, as (since August 2012) it is based on a standard Debian installation.
Ok, ok, now I guess you are curious about what virtual appliances are actually available. Of course you can find WordPress (e.g. here and here) as in this post's title, but also content management systems such as Drupal and Joomla, wikis as MediaWiki and MoinMoin, torrent servers, Web frameworks such as Django, developers stacks (e.g. *AMP, *APP), and revision control servers. So I guess this post is going to provide you a veeeery limited view on what you can do, but I hope it will at least stimulate some curiosity in you (then probably other posts will follow with new discoveries… ;-)).
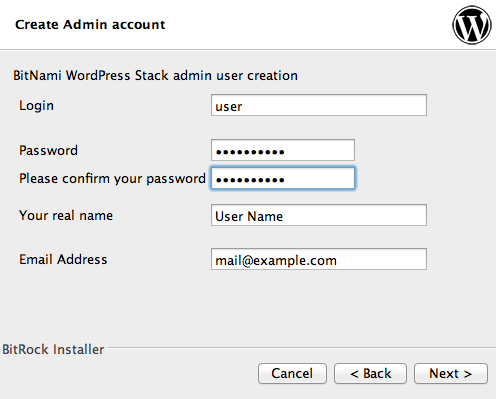
My first experiment with these VAs has been with Bitnami's WordPress. There are three ways to install it: using the native installer, with a VM image or directly deploying it in a cloud, e.g. on Windows Azure or AWS. The native installer on Mac is quite straightforward: you install it, provide (relatively) few configuration parameters, and voilà, you are ready to connect to your IP address (port 8080) and use your new WordPress or access your DB via phpmyadmin. All of this without being scared by the presence of all these new softwares in your system: everything is self-contained in one directory and does not interfere with existing software. For instance, I already have a MySQL instance running on my Mac and I just needed to provide a different port to make the two coexist.
This is very convenient if you want to test a new Web application. Its main limitation, however, is that it runs on your own PC, so if you want to make that WordPress website (or in general any Bitnami system you are running) accessible somewhere in the cloud, starting with a virtual appliance is going to make your life much easier.
Running the virtual appliance is also quite simple both with VMWare and with Virtualbox. In the latter case, converting the virtual disk from the VMDK (VMWare) to the VDI (Virtualbox) format is required. Be sure you check the virtual appliances quick start guide here, then perform the following steps.
Step 0: as a pre-requirement, I suppose you already have a recent version of VirtualBox installed. The one I am working with now is 4.2.6. If you don't, get one here.
Step 1: download the latest virtual appliance image file (e.g. for WordPress, get it here) and unzip it (at the time of writing this post, the filename is bitnami-wordpress-3.5-0-ubuntu-12.04.zip). This will create a new directory with the same name of the file (except the ".zip" extension, of course).
Step 2: check the contents of the new directory. You will find a list of files like the following one:
README.txt VirtualBox-4-README.txt bitnami-wordpress-3.5-0-ubuntu-12.04-VBOX3.mf bitnami-wordpress-3.5-0-ubuntu-12.04-VBOX3.ovf bitnami-wordpress-3.5-0-ubuntu-12.04-s001.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s002.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s003.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s004.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s005.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s006.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s007.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s008.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04-s009.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04.vmdk bitnami-wordpress-3.5-0-ubuntu-12.04.vmx
All those .vmdk files are parts of the hard disk image that needs to be converted in the format used by Virtualbox. To do this conversion open a terminal, cd to the new directory and enter the following command (all on one line):
VBoxManage clonehd bitnami-wordpress-3.5-0-ubuntu-12.04.vmdk bitnamiWordpress.vdi -format VDI
A new file called bitnamiWordpress.vdi will be created. This will be your new virtual machine's hard disk: you can move it to a place you will easily remember (see Step 5) and delete everything else from this dir.
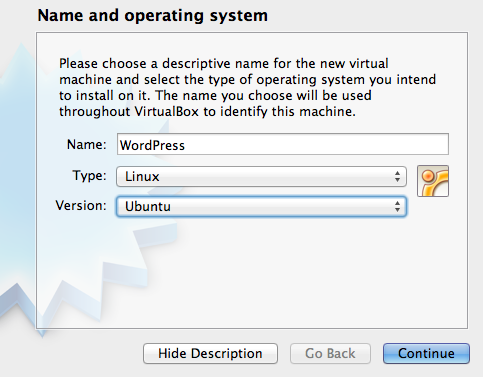
Step 3: open Virtualbox and hit the New button to create a new virtual machine. A window will open (see Figure 2) asking the name and OS for the new machine. Name it as you like, and choose Linux/Ubuntu as OS.
When asked for the amount of RAM, choose anything above or equal to 512MB. In the following window, choose "Do not add a virtual hard drive" and confirm your choice. After this step your new VM will be created, but you still have to explicitly link it to the disk image you previously created.
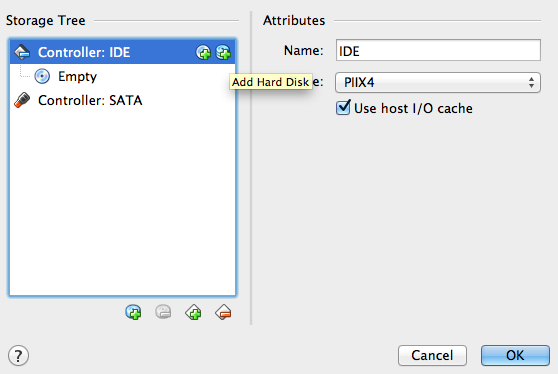
Step 4: choose your newly created VM and hit the Settings button. In the Storage tab you will find the list of disks attached to the VM (you should have only the "Empty" IDE CD if you followed the previous steps). Highlight Controller: IDE and click on the Add Hard Disk icon (see Figure 3). When asked whether to create a new disk or add an existing one choose the latter, then provide the path of the VDI image you created in Step 2.
Step 5: as a last configuration step, go to the Network tab and make sure your network adapter is enabled and configured as bridged (see Figure 4 - of course the adapter name might change according to which one is active in your system).
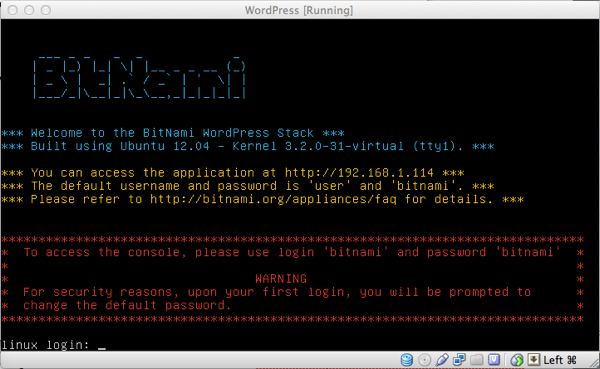
... Et voilà, the VM is ready: start it and if everything went fine you should be shown the following screen:
Note that you are provided an IP address (in this case 192.168.1.114): open your browser, connect to it and...
… enjoy! :-)
On Cracking
Some time ago I cracked my first Mac app. Overall it was a nice experience and reminded me of good old times. Here are some comments about it:
- it was the first commercial app (without considering MATLAB which I use for work) that I actually found useful after 1 year of Mac. I think that is good, because it means opensource software still satisfies most of my needs (or is it bad, because it means I am becoming a lazy hipster now?)
- the tutorial by fG! has been precious to me, especially to quickly find the tools of the trade. I suggest it to anyone willing to start reversing on Mac
- I am not half bad, after all: I managed to do that with the trial version of Hopper, so only deadlisting + time limit, and that added some spice to the game (I know everyone is thinking about Swordfish now... but no, there was no bj in the meanwhile ;-))
- cracking is still pure fun, especially when you find that the protection is hidden in functions with names purposely chosen to mislead you (no, I won't tell more details, see below)
- I have immediately bought the app: it was cheaper than going to a cinema and cracking it was more entertaining than the average blockbuster movie, plus I am left with a great program to use... That's what I call a bargain!
I still do not agree with Daniel Jalkut, the developer of MarsEdit: I think he wasted time on a trivial protection to sell some closed-source code he should have shared freely (as in freedom). But don't misunderstand me... Who am I to judge what somebody should or should not do? The only reason why I say this is that MarsEdit is a cool program (which btw I am using right now) and, while it is worth all the money I payed, not being able to see it open sourced is a real pity. But I respect Daniel's thought and I think his work deserved to be supported.
I know not all of you think about it this way, and probably I might have thought about it differently too, years ago. One thing, however, never changed: cracking/reversing is so much more than getting software for free, and if you stop there you are missing most of the fun ;-)
New TR: Multimodal diffusion geometry by joint diagonalization of Laplacians
Hi all,
this paper is something I am particularly happy to share, as it is the first report related to my new research theme (wow, this reminds me that I should update my research page!). The coolest aspect of this topic is that, despite looking different from my previous work, it actually has a lot of points in common with it.
As some of you may know, many previous works of mine heavily relied on different implementations of the concept of similarity (e.g. similarity between tags, between tourism destinations, and so on). This concept has many interpretations, depending on how it is translated into an actual distance for automatic calculation (this is what typically happens in practice, no matter how "semantic" your interpretation is supposed to be).
One of the main problems is: in a rich and social ecosystem like the Web is, it is frequent to find different ways to define/measure similarity between entities. For instance, two images could be considered similar according to some visual descriptors (e.g. SIFT, or color histograms), to tags associated with them (e.g. "lake", "holiday", "bw"), to some descriptive text (e.g. a Wikipedia page describing what is depicted), metadata (e.g. author, camera lens, etc.), and so on. Moreover, people might not agree on what is similar to what, as everyone has their own subjective way of categorizing stuff. The result is that often there is no single way to relate similar entities. This is sometimes a limit (how can we say that our method is the correct one?) but also an advantage: for instance, when entities need to be disambiguated it is useful to have different ways of describing/classifying them. This is, I believe, an important step towards (more or less) automatically understanding the semantics of data.
The concept I like most behind this work is that there are indeed ways to exploit these different measures of similarity and (pardon me if I banalize it too much) find some kind of average measure that takes all of them into account. This allows, for instance, to tell apart different acceptations of the same word as it can be applied in dissimilar contexts, or photos that share the same graphical features but are assigned different tags. Some (synthetic and real-data) examples are provided, and finally some friends of mine will understand why I have spent weeks talking about swimming tigers ;-). The paper abstract follows:
"We construct an extension of diffusion geometry to multiple modalities through joint approximate diagonalization of Laplacian matrices. This naturally extends classical data analysis tools based on spectral geometry, such as diffusion maps and spectral clustering. We provide several synthetic and real examples of manifold learning, retrieval, and clustering demonstrating that the joint diffusion geometry frequently better captures the inherent structure of multi-modal data. We also show that many previous attempts to construct multimodal spectral clustering can be seen as particular cases of joint approximate diagonalization of the Laplacians."
… and the full text is available on ArXiv. Enjoy, and remember that --especially in this case, as this is mostly new stuff for me-- comments are more than welcome :-)
New paper: Exploiting tag similarities to discover synonyms and homonyms in folksonomies
[This is post number 5 of the "2012 publications" series. Read here if you want to know more about this]
I have posted a new publication in the Research page:
Davide Eynard, Luca Mazzola, and Antonina Dattolo. Exploiting tag similarities to discover synonyms and homonyms in folksonomies.
"Tag-based systems are widely available thanks to their intrinsic advantages, such as self-organization, currency, and ease of use. Although they represent a precious source of semantic metadata, their utility is still limited. The inherent lexical ambiguities of tags strongly affect the extraction of structured knowledge and the quality of tag-based recommendation systems. In this paper, we propose a methodology for the analysis of tag-based systems, addressing tag synonymy and homonymy at the same time in a holistic approach: in more detail, we exploit a tripartite graph to reduce the problem of synonyms and homonyms; we apply a customized version of Tag Context Similarity to detect them, overcoming the limitations of current similarity metrics; finally, we propose the application of an overlapping clustering algorithm to detect contexts and homonymies, then evaluate its performances, and introduce a methodology for the interpretation of its results."
The editor (John Wiley & Sons, Ltd.) requested not to directly make the paper available online. However I have "the personal right to send or transmit individual copies of this PDF to colleagues upon their specific request provided no fee is charged, and further-provided that there is no systematic distribution of the Contribution, e.g. posting on a listserv, website or automated delivery." So, just drop me an email if you want to read it and I will send it to you (in a non-systematic way ;-))
New paper: Harvesting User Generated Picture Metadata To Understand Destination Similarity
[This is post number 4 of the "2012 publications" series. Read here if you want to know more about this]
I have posted a new publication in the Research page:
Alessandro Inversini, Davide Eynard. Harvesting User Generated Picture Metadata To Understand Destination Similarity.
This is an extension of a previous work for the Journal of Information Technology & Tourism, providing additional and updated information gathered with new user surveys.
"Pictures about tourism destinations are part of the contents shared online through social media by travelers. User-generated pictures shared in social networks carry additional information such as geotags and user descriptions of places that can be used to identify groups of similar destinations. This article investigates the possibility of defining destination similarities relying on implicit information already shared on the Web. Additionally, the possibility of recommending one city on the basis of a given set of pictures is explored. Flickr. com was used as a case study as it represents the most popular picture sharing website. The results indicate that it is possible to group similar destinations according to picture-related information, and recommending destinations without requiring users' profiles or sets of explicit preferences.".
New (old) paper: Finding similar destinations with Flickr Geotags
[This is post number 3 of the "2012 publications" series. Read here if you want to know more about this]
I have posted a new publication in the Research page:
Davide Eynard, Alessandro Inversini, and Leonardo Gentile (2012). Finding similar destinations with Flickr Geotags.
"The amount of geo-referenced information on the Web is increasing thanks to the large availability of location-aware mobile devices and map interfaces. In particular, in photo
collections like Flickr the coexistence of geographic metadata and text-based annotations (tags) can be exploited to infer new, useful information. This paper introduces a novel method to generate place profiles as vectors of user-provided tags from Flickr geo-referenced photos. These profiles can then be used to measure place similarity in terms of the distance between their matching vectors. A Web-based prototype has been implemented and used to analyze two distinct Flickr datasets, related to a chosen set of top tourism destinations. The system has been evaluated by real users with an online survey. Results show that our method is suitable to define similar destinations. Moreover, according to users, enriching place description with information from user activities provided better similarities".
New (old) paper: A Modular Framework to Learn Seed Ontologies from Text
[This is post number 2 of the "2012 publications" series. Read here if you want to know more about this]
I have posted a new publication in the Research page:
Davide Eynard, Matteo Matteucci, and Fabio Marfia (2012).A Modular Framework to Learn Seed Ontologies from Text
"Ontologies are the basic block of modern knowledge-based systems; however the effort and expertise required to develop them are often preventing their widespread adoption. In this chapter we present a tool for the automatic discovery of basic ontologies –we call them seed ontologies– starting from a corpus of documents related to a specific domain of knowledge. These seed ontologies are not meant for direct use, but they can be used to bootstrap the knowledge acquisition process by providing a selection of relevant terms and fundamental relationships. The tool is modular and it allows the integration of different methods/strategies in the indexing of the corpus, selection of relevant terms, discovery of hierarchies and other relationships among terms. Like any induction process, also ontology learning from text is prone to errors, so we do not expect from our tool a 100% correct ontology; according to our evaluation the result is more close to 80%, but this should be enough for a domain expert to complete the work with limited effort and in a short time".
This work is part of the book "Semi-Automatic Ontology Development: Processes and Resources" edited by Maria Teresa Pazienza and Armando Stellato.
Octave clustering demo part 3: spectral clustering
[This post is part of the Octave clustering demo series]
This is (currently) the last of my posts devoted to clustering demos. If you haven't downloaded the file containing Octave code yet, you can get it here. If you want to read the previous articles, here they are: part 0 - part 1 - part 2.
The last demo in the package shows you how spectral clustering works. Spectral Clustering is a relatively recent approach to clustering that I found very interesting, especially because it addresses some of the limitations of k-means but, at the same time, it relies on k-means itself! What it does in practice is finding a new space where localities are preserved, emphasizing both the cohesion and the separation of clusters, thus allowing k-means to work at its best. If you are curious and want to delve deeper into this topic, you will find more material in the following page: Paper Review: A Tutorial on Spectral Clustering.
I was quite surprised not to find ready code for spectral clustering in Octave, but probably I just had not searched (well) enough. By the way, if you came here searching for it here is an(other?) implementation, together with some examples and data to play with: feel free to try it and to leave your feedback!
The spectralDemo function can be called as follows:
spectralDemo(dataset,nn,t)
where dataset is the usual dataset path+name, while nn and t are parameters used to build the (weighted) adjacency matrix describing similarity relationships between data points. Respectively, nn specifies the number of nearest neighbors for a point (a point is connected to another if it appears as one of its top nn nearest neighbors) and t is the parameter for the Gaussian similarity function s(xi,xj)=exp(-(xi-xj)^2 / t). My suggestion is to play with both parameters, but once you understood how they work you can just keep t=0 for the automatic tuning of the kernel and focus only on nn. Good values of nn range between 10 and 40, but of course you are free to test others (but keep in mind that the bigger the value, the slower the whole algorithm is! Can you say why?). The script performs the following tasks:
- it calculates the weighted adjacency matrix and plots both the distances between points and the weights between nodes in the adjacency graph (this allows one to inspect whether parameters need to be trimmed to have a more/less connected graph, and also to understand when the graph approach might work better than a classical euclidean distance approach);
- it builds the graph Laplacian and calculates its eigenvalues and eigenvectors. Then, it plots eigenvalues for inspection (this allows one to understand --if the dataset is clean enough-- how many connected components/natural clusters are present in the graph);
- to compare results between k-means and spectral clustering, it runs k-means both in the euclidean space and in the eigenspace built out of the top k eigenvectors, then shows both clusterings with related SSEs and accuracies.
And now, here are the usual maieutical questions:
- what are the datasets in which spectral clustering performs definitely better than k-means?
- how much do the results of spectral clustering depend on the input parameters?
- how would you evaluate the quality of a labeling done with spectral clustering? How would you apply that to find which is the best number of nearest neighbors to take into account?
- how often (according to your tests with different datasets) does the rule "the number of 0-valued eigenvalues matches the number of clusters" holds? How ofted does its "relaxed version" hold? (if the question is not clear check spectral clustering notes/papers)
- how worth would be to use algorithms other than k-means to do clustering in the eigenspace?
That's all... have fun with the demos and with spectral clustering :-)